Grafos dirigidos con Matrices de adyacencia

Grafos dirigidos.

G=(V,A) un grafo dirigido con |V|=n .Se define la matriz de adyacencia o booleana asociada a G como Bnxn con



Como se ve,se asocia cada fila y cada columna a un vértice y los elementos bi,j de la matriz son 1 si existe el arco (i,j) y 0 en caso contrario.
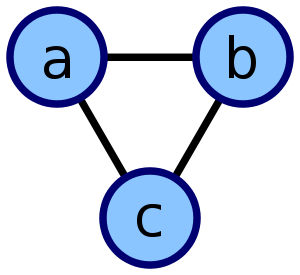
Grafos no dirigidos.

G=(V,A) un grafo no dirigido con |V|=n .Se define la matriz de adyacencia o booleana asociada a G como Bnxn con:



La matriz B es simetrica con 1 en las posiciones ij y ji si existe la arista (i,j).

EJEMPLO:

Si el grafo es etiquetado,entonces tanto b_i,j como b_i,j representan al coste o valor asociado al arco (i,j) y se suelen denominar matrices de coste. Si el arco (i,j) no pertenece a A entonces se asigna b_i,j o b_i,j un valor que no puede ser utilizado como una etiqueta valida.

Creo que La principal ventaja de la matriz de adyacencia es que el orden de eficiencia de las operaciones de obtencion de etiqueta de un arco o ver si dos vertices estan conectados son independientes del número de vértices y de arcos. Por el contrario, existen dos grandes inconvenientes:

• Es una representación orientada hacia grafos que no modifica el número de sus vertices ya que una matriz no permite que se le o supriman filas o columnas.
• Se puede producir un gran derroche de memoria en grafos poco densos (con gran número de vértices y escaso número de arcos).

Para evitar estos inconvenientes se introduce otra representación: las listas de adyacencia.

Bibliografia:

http://www.monografias.com/trabajos16/grafos/grafos.shtml

http://decsai.ugr.es/~jfv/ed1/tedi/cdrom/docs/grafos.htm

http://docencia.udea.edu.co/regionalizacion/teoriaderedes/representacionu1.html